High Performance Computing & Numerical Analysis
Faculty Researchers:
Donald Schwendeman, Fengyan Li, Jeffrey Banks
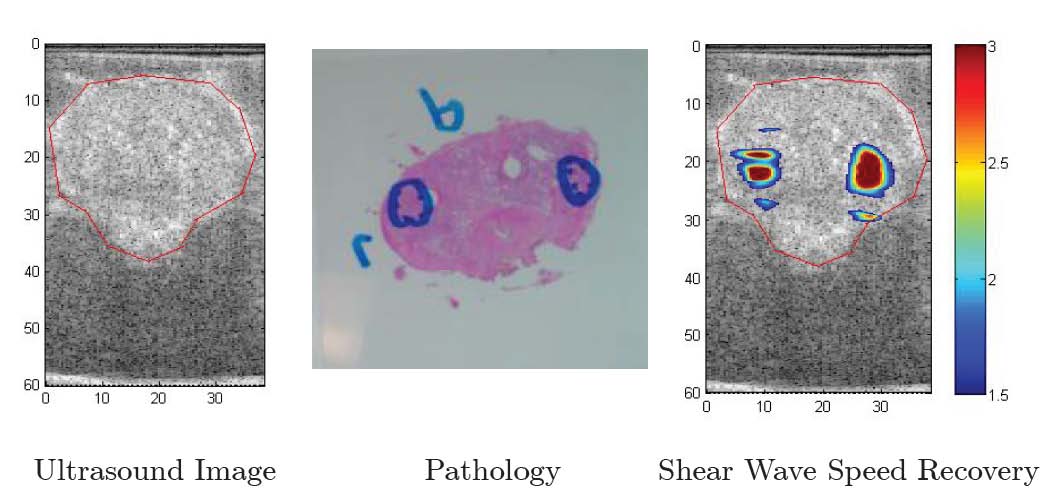
Research in high performance computing and numerical analysis involves the development of algorithms designed to compute solutions of difficult, often nonlinear, mathematical problems spanning a wide range of applications. An essential element of the research concerns the analysis of the algorithms, which seeks to uncover important properties of the methods, such as stability and convergence, so that the algorithms can be employed with a clear understanding of their behavior and accuracy. To obtain well-resolved solutions of problems in complex multidimensional configurations, high-performance computers, such as those available at Rensselaer’s CCI, are often needed, and an exciting aspect of the research involves implementing algorithms effectively and efficiently for such platforms.
Faculty in the Department of Mathematical Sciences are active in this area of research. Recent work has led, for example, to the development of a wide class of stable and efficient partitioned algorithms for fluid-structure interaction problems, high-order accurate variational finite-difference methods, exactly divergence-free central discontinuous Galerkin finite-element methods, energy-conserving or asymptotically preserving high-order methods for kinetic equations, upwind methods for hyperbolic equations in second-order form, high-order conservative methods for Maxwell’s equations, and numerical methods in differential geometry.